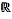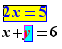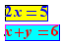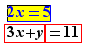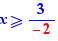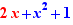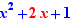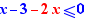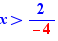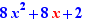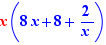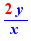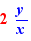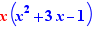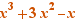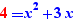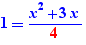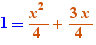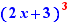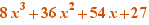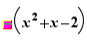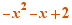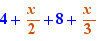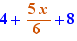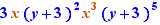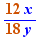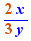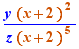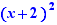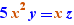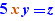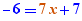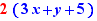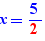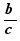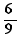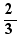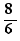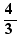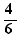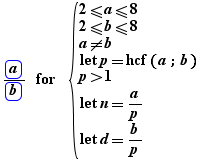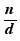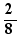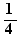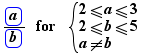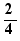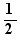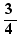EpsilonWriter version 2.7
Manual of Dynamic Algebra
January 29, 2016
Document written with EpsilonWriter
Summary
Epsilonwriter allows doing exact and approached calculations by button, click and drag.
These are calculation steps, with explanations.
It also allows generating formulas from a formula containing parameters.
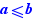
Calculations can be made on the real or complex numbers. The first button of the "Calculation" panel indicates the field of numbers, e.g.  . Change the field by clicking on this button. The entire document works in this field. A document of another tab can have a different field. When the field is
. Change the field by clicking on this button. The entire document works in this field. A document of another tab can have a different field. When the field is 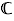 , i is a number verifying
, i is a number verifying  When the field is
When the field is 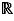 , i is a variable.
, i is a variable.
1. Choice of the tools, parameters
The "Calculation" panel allows choosing the calculation tools:
- Numerical calculations can be done on integers, decimal, or rational numbers,
- The calculation tools used are determined by the level of dynamic algebra whose possible values are: pedagogical, low, medium, strong, customed.
The trigger of a click-calculation is controlled by a choice liste in the "Calculate" panel.
When "Dynamic Algebra: Custom" is selected, EpsilonWriter shows the different dynamic algebra mechanisms so that the user chooses those he/she wants to use. These choices are stored and can be changed by re-selecting "Dynamic Algebra: Custom".
The choice of mechanisms are application settings. It is possible to "View application parameters" with the "Options" menu and also display a "Table of parameters" that shows the values of these parameters for all dynamic algebra modes. This table is also at:
It is possible to associate parameters to a document so that students can only use certain tools. See the EpsilonWriter manual:
The "Calculation" panel allows choosing the form of explanations.
2. Basic calculations by click and button
2.1. Basic exact calculation by click on an expression or use of a button
Calculation by click includes exact numerical computation, integer factorisation, expand and simplify, linear equations solving, production schemes for solving equations of degree 2 and 3, the definition conditions of rational functions, the passage of certain logical conditions to solution sets, the computing of limits, the passage of factored rational fractions into sign tables, the calculation of derivatives, the passage of a form 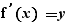 , where y is a factored rational fraction to a variation table.
, where y is a factored rational fraction to a variation table.
To make an exact calculation, you can select an expression or sub-expression. If the Click-calculation mode is enable and there are possible calculations by click, they are listed in a tooltip. When there is only one, a click on the tooltip applies the proposed calculation. When there are several, a Ctrl+Clik on the selected expression displays a popup menu in order to choose the calculation to perform.
If "Duplicate when calculations" is checked, the result is displayed below. If it is not checked, it replaces the expression to calculate.
The choice list "Duplicate ..." of the Calculation panel indicates whether the calculation result should be displayed beside or below the expression to calculate.
The choice of field (integer, decimal or rational) is done with a list of choices in the "Calculation" panel.
2.2. Calculation by click on an operator
When the mouse flies over an operator, if this mode is enabled and if there are possible calculations by click, they are listed in a tooltip.
A Ctrl+Click on an operator asks to calculate the expression of this operator.
Example, Ctrl+Click on + in  produces
produces 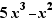
2.3. Basic proposed calculations
Numerical calculations, expansions and simplifications are proposed, mainly for rational expressions.
Solving linear equations of one variable is also proposed.
The  button allows you to perform approximate calculations.
button allows you to perform approximate calculations.
The  buttons can convert decimals into fractions and fractions into decimals.
buttons can convert decimals into fractions and fractions into decimals.
The  button allows you to duplicate the expression; it is useful when you do not duplicate the expression automatically for each calculation.
button allows you to duplicate the expression; it is useful when you do not duplicate the expression automatically for each calculation.
2.4. Calculations proposed for quadratic polynomials and equations of one variable
Depending of the coefficients, the following actions are proposed for  :
:
- Complete the square,
- Factor with 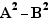 (when the field is
(when the field is  )
)
- Generate the discriminant formula to factor the polynomial (when the field is  ) .
) .
EpsilonWriter proposes also to generate the discriminant formulas for solving 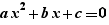 (when the field is
(when the field is 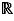 )
)
See demos at: http://epsilonwriter.com
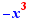
2.5. Calculations proposed for cubic polynomials and equations of one variable (when the field is 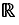 )
)
EpsilonWriter proposes to generate the Cardan's formulas for factoring 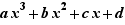 and for solving
and for solving 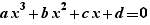
See demos at: http://epsilonwriter.com
2.6. Sign tables (when the field is 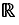 )
)
For many factored rational expressions like 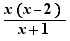 , EpsilonWriter proposes to build a sign table (a filled table or a table to fill).
, EpsilonWriter proposes to build a sign table (a filled table or a table to fill).
2.7. Definition conditions and definition sets of functions (when the field is 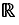 )
)
When a function is defined with an equal sign like  EpsilonWriter proposes to produce the definition conditions, in this example:
EpsilonWriter proposes to produce the definition conditions, in this example:
Defined when: 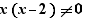
It is necessary to use the true function notations of EpsilonWriter, i.e., one of the letter f, g and h in straight shape with parentheses (when the letters are in italics, they represent variables, not functions).
When definitions conditions are in factored forms, EpsilonWriter generally proposes to generate a corresponding set. For the above condition:
Set: ]-∞;0[∪]0;2[∪]2;+∞[
2.8. Limits of rational fractions (when the field is 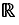 )
)
For limits of rational fractions at infinity, like 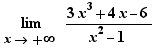 , EpsilonWriter applies the highest degree theorem.
, EpsilonWriter applies the highest degree theorem.
For limits of rational fractions at finite values, like 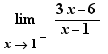 EpsilonWriter replaces the variable x by the
EpsilonWriter replaces the variable x by the 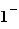 notation and allows you to perform limit calculation on this notation.
notation and allows you to perform limit calculation on this notation.
2.9. Calculation of derivatives (when the field is 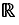 )
)
The notation for derivatives can be 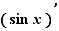 or
or 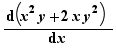
EpsilonWriter calculates a step of deriving when a Ctrl-Click is made on the derivative operator.
Almost all usual functions can be derived.
2.10. Variation tables of rational fractions (when the field is 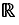 )
)
When a derivative is expressed in a factored form with an equal sign, like 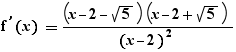 , EpsilonWriter generally proposes to produce a variation table (a filled table, except limits, min and max values, or a table to fill).
, EpsilonWriter generally proposes to produce a variation table (a filled table, except limits, min and max values, or a table to fill).
It is necessary to use the true function notation of EpsilonWriter, i.e., one of the letter f, g and h in straight shape with parentheses (when the letters are in italics, they represent variables, not functions).
2.11. Simplification of sets of real numbers (when the field is 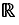 )
)
Sets of real numbers, expressed as combinations of intervals and finite sets, like ![(]-∞;0] \ ]-5;-3[)∩]-8;-1[∪{-6;6}](_Manuel-AD-en.html/image29.png) can be simplified.
can be simplified.
3. The external drag&drop
Works with the "Dynamic Algebra: medium and strong".
We say that we make an external drag&drop when the selected expression and the location to drop are not in the same mathematical expression, for example, if we have:
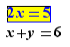
And if we make a drag&drop of the selected expression somewhere in  we are in external drag&drop. There is no mathematical link between
we are in external drag&drop. There is no mathematical link between 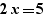 and
and  for EpsilonWriter. There is just an equality below the other one.
for EpsilonWriter. There is just an equality below the other one.
3.1. Indicating the location to drop in external drag&drop
During the drag, when the mouse cursor:
- flies over an atomic element, this one is shown as a second selection in blue,
- flies over an operator, the expression of this one is shown as a second selection in blue,
- otherwise, a drop cursor is shown.
Here are 4 examples:
|
|
|
|
When the drop is possible, a popup menu displays the possibilities: the resulting formula and the explanation of the action.
3.2. The completion of the external drag&drop
To accept a drop proposal shown in the pop-up, it is necessary to release the mouse button. If there was a single proposal in the pop-up, this one is immediately applied. If there were several, the pop-up remains shown and it is necessary to choose by clicking or using the return key, or to cancel with Ctrl+Z.
Color code of the buttons of the pop-up:
- Green: mathematical operation providing equivalence (see explanations in section equivalence),
- Red: mathematical operation not providing equivalence a priori.
The options:
Duplicate when calculations
Explain calculation
apply to external drag&drop.
3.3. The possible operations for external drag&drop
Substitution
When the selected expression is a substitution, that is:
- An equality of the shape 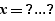 or
or  , example
, example 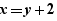
- simultaneous equalities of this type, example: 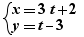 counterexample:
counterexample: 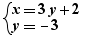 in this last cae, variable y expressed in the second equality being in the first equality, it si not considered as a substitution,
in this last cae, variable y expressed in the second equality being in the first equality, it si not considered as a substitution,
EpsilonWriter suggests applying the substitution if the location of the drop is an expression containing variables of the substitution.
Equivalence
In that case, there is a priori no equivalence.
There is equivalence however in the case of a simultaneous equations, if the selection is an equation of the simultaneous equations.
Substitution of a variable by an expression
When the selected expression is an expression, eg 4 or 2x+1 , if the location of the drop is a variable, EpsilonWriter proposes to carry out a substitution of the variable by the expression.
Addition or subtraction to both sides of relations
When the selected expression is an equality or an inequality and when the location of the drop is an equality or an inequality,
EpsilonWriter proposes an addition and a subtraction to both sides if it has of the meaning, i.e., if the result is implied by both relations.
Equivalence
In that case, there is a priori no equivalence.
Addition, subtraction, multiplication or division of/by an expression to both sides of relations
When the selected expression is a numerical expression with possibly variables (not a relation) and the location of the drop is an equality or an inequality,
EpsilonWriter suggests adding, subtracting, multiplying, dividing both sides by the expression.
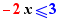
For inequalities, it is only when the selected expression is a number (with change of the direction of the inequality sign when the number is negative).
Equivalence
In that case, there is equivalence between the initial relation and the resulting relation, except for multiplication by 0 (division by 0 is not proposed). This equivalent can require the addition by the user of conditions as  if we divide both members of an equality by x
if we divide both members of an equality by x
4. The "assimilated" external drag&drop
Works with the "Dynamic Algebra: medium and strong" options.
When the selected expression and the location of the drop are not in the same numerical expression (with variables) or equality or inequality, we consider that we are in a situation similar to the external drag&drop and the behavior of the drag&drop is identical to the external drag&drop.
This is the case for simultaneous equalities or inequalities:
Example: 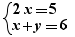 when
when 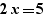 is dropped on y or on
is dropped on y or on 
For simultaneous equalities or inequalities, There is however a difference at the level of the equivalence:
- In the case of a substitution, there is equivalence between the system of origin and the obtained system,
- In the case "Addition or subtraction to both side of relations", there is equivalence between the system of origin and the obtained system, when the added or subtracted relation is an equality.
5. The internal drag&drop
When the selected expression and the location to drop are in the same numerical expression (with or without variables) or in the same equality or inequality, we are in the case of the internal drag&drop.
The drag&drop works according to the "Dynamic Algebra" option:
- With the "Dynamic Algebra: Pedagogical" option, only basic moves are proposed. A basic move of an expression a is a move which preserves a or replaces it by -a or 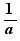 and preserves the rest of the expression with one possible exception: if there is an inequality, its orientation can be reversed. With this option, the actions that do not produce basic moves are indicated.
and preserves the rest of the expression with one possible exception: if there is an inequality, its orientation can be reversed. With this option, the actions that do not produce basic moves are indicated.
- With the "Dynamic Algebra: Light" option, simple and useful (basic or not) moves are proposed.
- With the "Dynamic Algebra: Medium" option, more moves are proposed.
- With the "Dynamic Algebra: Strong" option, all the possible moves with EpsilonWriter are proposed.
See the detailed list of moves for each option at http://epsilonwriter.com
The "Describe the dynamic algebra gesture" option allows you describing certain gestures. This description is added to the mathematical explanation.
Example: the movement of a negative factor from a side of the inequality to other one provides the description and the explanation below:
|
Gesture: Multiplicative move of a negative expression to the other side, the factor becomes divisor, the inequality sign is reversed Explanation: division of both sides by -2 |
Indicating the location to drop in internal drag&drop, completion and display
The indication of the location to drop has two possible forms:
- a cursor, for example  for a drop before 4 which produces
for a drop before 4 which produces 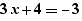
- a blue selected expression for a combination of the moved expression with it, for example  which produces
which produces 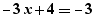
When the drop is possible, a pop-up shows the possibilities. It also displays regular editing drops with the main operators.
There is always equivalence with internal dra&drop, but this equivalence can require the addition by the user of conditions as  if we divide both members of an equality by x
if we divide both members of an equality by x
With the Dynamic Algebra: Pedagogical option, some refused drops are described. For example, given 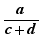 , sif we try to move c to the front of the fraction, we get: No basic additive exit of the denominator.
, sif we try to move c to the front of the fraction, we get: No basic additive exit of the denominator.
The operations of internal drag&drop
The elementary operations currently implemented belong to 4 categories:
- Moving in an expression,
- Exiting from an expression,
- Entering into an expression,
- Combination of the selected expression with another expression.
These operations are made with a status of the selected expression which can be:
- Adder: we will also speak of additive term or additive operation,
- Multiplier: we will also speak of factor or multiplicative operation,
- divisor,
- exponent.
In very numerous cases, these elementary operations can be combined.
During the drag, when we are in a case of combination, the second element of the combination is shown as a second selection in blue. In other cases, a cursor for drop is shown.
5.1. Examples of movement
An argument of a sum or a product can be moved in this sum or this product.
|
Explanation: commutativity |
A side of a relation, or an additive term of a side, can be moved in an additive way to the other side. It is replaced by its opposite.
|
Gesture: Additive move to the other side, changing sign Explanation: Addition to both sides of -2x |
A side of a relation, or a factor of a side, can be moved in a multiplicative way to the other side. It must not be equal to 0. In the case of an inequality, it cannot have variables. It becomes divisor. The direction of the relations is change if necessary.
|
Gesture: Multiplicative move of a negative expression to the other side, the factor becomes divisor, the inequality sign is reversed Explanation: division of both sides by -4 |
|
Gesture: Multiplicative move to the other side, the factor becomes divisor Explanation: division of both sides by 4x |
If we move 4x in 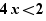 , there is no proposal as divisor because 4x is not constant.
, there is no proposal as divisor because 4x is not constant.
An exponent 2 of a side of a relation can be moved in a multiplicative way to the other side if the other side is an expression without variable. There is then production of a square root and of an "or" between two equalities.
|
Explanation: decomposition of an equation |
5.2. Examples of exit from an expression
A term of a sum or a factor of a term of a sum, can go out of the sum as factor. It must not be equal to 0.
|
Explanation: factorising x |
A numerator or a factor of a numerator can go out of the numerator as factor.
|
Explanation: The factor 2 of the numerator becomes the factor of the fraction |
Factoring HCF
When we ask to factor out a positive integer n in a sum, if the terms of the sum have coefficients having a HCF different from 1 and n , EpsilonWriter suggests in addtiton to factor out the HCF.
This operation does not function with the Pedagogical Dynamic Algebra option.
|
Explanation: factoring HCF: 3 |
5.3. Examples of enter into an expression
A factor can enter into a sum, an expansion is then applied.
|
Explanation: expansion |
A divisor can enter into a sum, an expansion is then applied.
Example, in combination with a movement in an equality:
|
Gesture: Multiplicative move to the other side, the factor becomes divisor Explanation: division of both sides by 4 |
|
Explanation: expansion |
An exponent 2 or 3 over a sum of two terms can enter the sum, an expansion is then applied
Example :
|
Development |
This operation does not function with the Pedagogical Dynamic Algebra option.
An exponent over a product, an opposite or a power can enter the argument.
Examples :
|
Power of an opposite |
5.4. The case of sign -
A selected sign - can be the object of a drag&drop, it is as if -1 has been selected with a status of factor.
|
Explanation: Expansion |
5.5. Combinations: additive combinations
Notion of like terms
Two terms of a sum are like terms when each is one of the forms 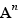 ,
, 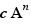 , with the same A and the same n , A being any expressions, c a number and n an integer which can be omitted if it is 1 .
, with the same A and the same n , A being any expressions, c a number and n an integer which can be omitted if it is 1 .
Examples:
x , -x , 3x , 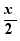 ,
,  ,
, 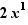 are like terms
are like terms
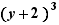 ,
, 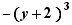 ,
, 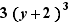 ,
, 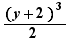 ,
, 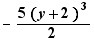 are like terms
are like terms
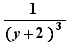 ,
, 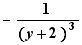 ,
, 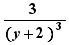 ,
, 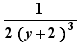 ,
, 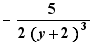 are like terms
are like terms
When the option Combination of positive and negative exponents is active,  and
and 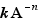 with the same A and the same n are also considered as like terms
with the same A and the same n are also considered as like terms
A term of a sum can be moved in this sum over a like term so that both are replaced by the calculated sum by taking into account the "Calculate (exact...)" option.
|
collecting like terms |
A term of a sum of the form nA can be moved in this sum over term of a sum of the form 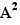 to produce a completion of the square.
to produce a completion of the square.
|
completing the square |
5.6. Combinations: multiplicative combinations
Notion of like factors
Two factor of a product are like factors when each is one of the forms A , 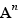 , with the same A , A being any expression, n an integer
, with the same A , A being any expression, n an integer
example:
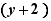 ,
, 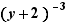 ,
, 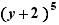 are like factors
are like factors
When the option Combination of positive and negative exponents is active, A , 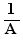 ,
, 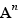 ,
, 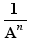 with the same A are also considered as like factors.
with the same A are also considered as like factors.
A factor of a product can be moved in this product over a like factor so that both are replaced by the calculated product by taking into account the "Calculate (exact...)" option.
|
multiplying like factors |
5.7. Combinations: simplifications of fractions
An integer which is factor of the numerator/denominator of a fraction can be moved on an integer which is factor of the denominator/numerator of the fraction so that both are simplified by the HCF.
|
Simplification by 6 |
An expression of the form X or  which is factor of the numerator/denominator of a fraction can be moved on an expression of the form X or
which is factor of the numerator/denominator of a fraction can be moved on an expression of the form X or  which is factor of the denominator/numerator of the fraction so that both are simplified by the
which is factor of the denominator/numerator of the fraction so that both are simplified by the 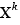 with a maximum k.
with a maximum k.
|
Simplification by |
What is "being a factor of the numerator" above?
It is been X in one of the forms 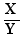
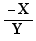
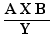
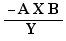 , idem for factor of the denominator.
, idem for factor of the denominator.
5.8. Combinations: multiplicative simplifications of relations
Simplifications similar to the simplifications of fractions can be made on relations.
For the inequalities: the expression by which we simplify has to be constant and when its sign is negative, the direction of the inequality is changed.
Attention: when the simplification is made by a not constant expression in an equation, there are generally loss solutions, for example, if we simplify the equation  by x we lose the solution
by x we lose the solution 
It belongs to the user to manage the conditions which accompany the operations. In the case above, the user can add "when  " and manage besides the case x=0. The user replace the operation and by a treatment which does not separate cases.
" and manage besides the case x=0. The user replace the operation and by a treatment which does not separate cases.
Example, sign - is selected by Ctrl+Clic and is move on the other sign -
|
simplification of minus signs |
|
division of both sides by x |
5.9. Combinations: additive simplifications of relations
Additive simplifications similar to the additive combinations in sums can be made on relations.
|
Addition to both sides of -5x |
6. The equivalence
The equivalence indicated by EpsilonWriter in the pop-up and the explanations:
When there is equivalence, buttons are green in the pop-up and the arrow of the explanation is sinuous and green: 
The equivalence mentioned in the internal and external drag&drop is equivalence brought by the context and the interpretation of the gesture:
In certain contexts, we know that there is equivalence modulo of the conditions to be added if necessary
In a more precise way:
An indication of equivalence means that the context (internal or external, nature of the transformation) allow you to assert it, modulo conditions to be added if necessary.
Attention, there can sometimes be equivalence when the context does not indicate it, for example, in the simultaneous inequalities  the addition sides to sides of the inequalities produces
the addition sides to sides of the inequalities produces 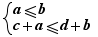 is not an operation generally producing equivalence, only an implication, but in the particular case
is not an operation generally producing equivalence, only an implication, but in the particular case 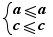 there is however equivalence and epsilowriter does not indique. Thus the indicated equivalence is not equivalence between initial expression and transformed expression (as it is the case in Aplusix) but an equivalence brought by the context and the nature of the gesture.
there is however equivalence and epsilowriter does not indique. Thus the indicated equivalence is not equivalence between initial expression and transformed expression (as it is the case in Aplusix) but an equivalence brought by the context and the nature of the gesture.
7. The explanations
7.1. Meaning of arrows
The explanation with the right arrow → below:
|
addition side with side of |
is read:
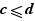 has been replaced by
has been replaced by 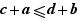 . Arrow → indicates the replacement, nothing more.
. Arrow → indicates the replacement, nothing more.
The explanation with the sinuous right arrow  below:
below:
|
Explanation: expansion |
is read:
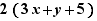 has been replaced by 6x+2y+10 applying an expansion operation and there is equivalence with possibly conditions to be added.
has been replaced by 6x+2y+10 applying an expansion operation and there is equivalence with possibly conditions to be added.
In that case, the equivalence can be between both mentioned expressions or at the level of simultaneous equations and inequalities which contains both arguments of the operation.
7.2. The color code
For the movements, the entrances, the exits, red indicates the moved element.
Example:
|
division of both sides by 2 |
In certain cases, the element is not moved in the result. A more complex operation is made, its result is indicated in brown, example:
|
Explanation: expansion |
8. Undo
When we do not make duplication and when we do not ask for explanation, the result of the operation simply replaces the expression. In that case, "undo" (Ctrl+Z) goes back to the situation before the operation.
When we make duplication or when we ask for an explanation, there is production of additional lines. In that case, the first "undo" places in the situation "operation without duplication and without explanation" and the second "undo" goes back to the situation before the operation.
9. Delete, modify explanations
Explanations are provided in a paragraph or in a table. They are editable.
10. Generation of formulas
10.1. Principle
The special formula operator "for" enables the generation of formulas instantiating a formula containing parameters. For example, if one writes the formula:
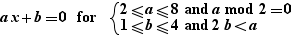
and if a Ctrl+Click on "for" is done, one gets:
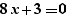

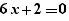
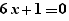
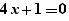
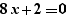
on the line below.
The button panel "Generation" gives access to tools for generating formulas.
10.2. The two ways of generating formulas
The first way consists in doing a Ctrl+Click on "for". The result is added to the row below.
The second way consists in using the "Generate" button of the "Generation" panel. Generating therefore relates to a paragraph or a table which must be selected before (it is sufficient to select a portion of the paragraph or table).
Example in the case of a paragraph with the following line:
The equation 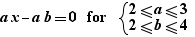 has solution b
has solution b
By selecting a part of the line and clicking on "Generate", one gets:
The equation 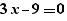 has solution 3
has solution 3
The equation  has solution 4
has solution 4
The equation 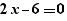 has solution 3
has solution 3
The equation 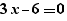 has solution 2
has solution 2
The equation 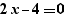 has solution 2
has solution 2
The equation 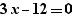 has solution 4
has solution 4
Note that the result replaces the original line.
Example in the case of a table (small blue frames are explained below):
fraction |
simplifies by |
the result is |
|
a |
|
By selecting a part of the table and clicking on "Generate", we get a table whose beginning is:
fraction |
simplifies by |
the result is |
|
3 |
|
|
2 |
|
|
2 |
|
Remarks:
- The result replaces the original table,
- If the table has several lines: each line that does not contain a for is copied to the result; each line that contains a for is developed in the result.
10.3. Syntax and functioning of "for"
One for includes parameters. These are letters which are to the right, in a double inequality with integer limits, eg 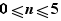 This means that n is a parameter and its initial values are integers expressed by this formula. Possible settings are letters for Latin and Greek letters, uppercase or lowercase, with the exception of two constants e and π .
This means that n is a parameter and its initial values are integers expressed by this formula. Possible settings are letters for Latin and Greek letters, uppercase or lowercase, with the exception of two constants e and π .
The right argument of "for" may combine the three forms of "and" 
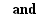 ∧ anyway.
∧ anyway.
The conditions not specifying the initial values of parameters may include or and not.
The formulas are generated randomly.
A special operator named "number" is used to limit the number of formulas to be generated. For example:
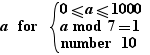
provides 10 numbers between 0 and 1000 having the remainder of division by 7 equal to 1.
It is possible to use the mod operator (remainder of the division), HCF and LCM, which are very useful in some cases.
It is also possible to use the prime logical operator, 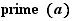 is true when a is a prime number.
is true when a is a prime number.
The let operator, usable on the right side of for, can build intermediate formulas.
For example in the for of the table below, one expresses in parameters constructed with let, values which are used in some cells:
fraction |
simplification par |
simplification par |
simplified denominator |
simplified fraction |
|
p |
n |
d |
|
"Generate" apply to this table provides a table that begins:
fraction |
simplification par |
simplification par |
simplified denominator |
simplified fraction |
|
2 |
4 |
3 |
|
|
2 |
1 |
4 |
|
10.4. Order of conditions
Double inequalities that define the initial values of the parameters must be placed first.
The conditions related to the parameters defined by "let" should be placed after the "let" defining these parameters.
10.5. Operators  and
and 
When generating a for, simple calculations are performed on expressions. Thus, the generation of 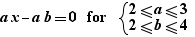 provides:
provides:

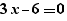
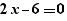
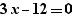
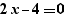
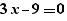
and not:
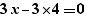
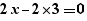
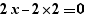
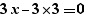

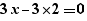
The  and
and  operators are calculating operators. When they are placed on sub-expressions, they mean "performing simple calculations" on framed parts and do not perform calculations elsewhere.
operators are calculating operators. When they are placed on sub-expressions, they mean "performing simple calculations" on framed parts and do not perform calculations elsewhere.
Their difference concerns decimal numbers: with blue operator, they are put in the form of fractions; with the pink operator, they are expressed with decimal notation.
This is illustrated by the table below:
unsimplified fraction |
simplified fraction in fraction form |
if possible decimal notation |
|
|
|
which generation provides a table that begins:
unsimplified fraction |
simplified fraction in fraction form |
if possible decimal notation |
|
|
0.5 |
|
|
0.75 |
|
|
|
Note: In the above example,  requests not to do simple calculations on a and b , but there are none to do because they are integers, but it also asks also not to do simple calculations elsewhere, not to simplify the fraction.
requests not to do simple calculations on a and b , but there are none to do because they are integers, but it also asks also not to do simple calculations elsewhere, not to simplify the fraction.