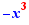
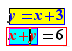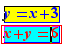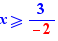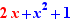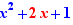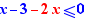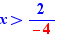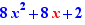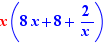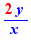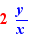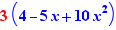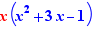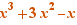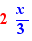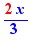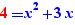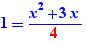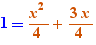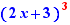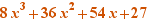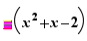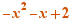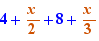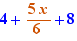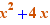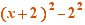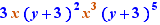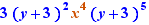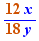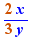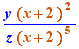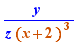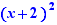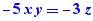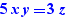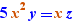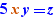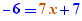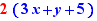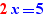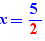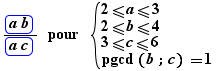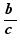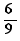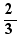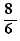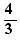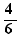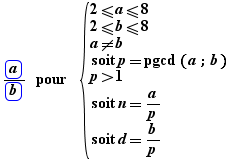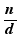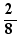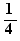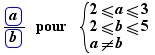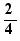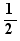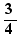EpsilonWriter version 2.7
Manuel d'algèbre dynamique
29 janvier 2016
Document rédigé avec EpsilonWriter
Sommaire
EpsilonWriter permet de faire des calculs exacts ou approchés par bouton, clic et glisser-déposer.
Ce sont des calculs par étapes, avec des explications.
Il permet aussi d'engendrer des formules à partir d'une formule comptant des paramètres.
Les calculs peuvent se faire sur les nombres réels ou complexes. Le premier bouton du panneau "Calcul" indique le domaine des nombres, par exemple :  . On change le domaine en cliquant sur ce bouton. Tout le document fonctionne sur ce domaine. Un document d'un autre onglet peut avoir un domaine différent. Quand le domaine est
. On change le domaine en cliquant sur ce bouton. Tout le document fonctionne sur ce domaine. Un document d'un autre onglet peut avoir un domaine différent. Quand le domaine est  , i est un nombre vérifiant
, i est un nombre vérifiant 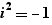 . Quand le domaine est
. Quand le domaine est 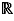 , i est une variable.
, i est une variable.
1. Choix des outils, paramètres
Le panneau "Calcul" permet de choisir les outils de calcul :
- les calculs numériques peuvent se faire sur les entiers, les décimaux ou les rationnels,
- les outils de calculs utilisables sont déterminés par le niveau d'algèbre dynamique dont les valeurs possibles sont : pédagogique, faible, moyen, fort, personnalisé.
Le déclenchement du calcul par clic est piloté par une liste de choix du panneau "Calcul" :
Lorsque "Algèbre dynamique : Personnalisé" est sélectionnée, EpsilonWriter présente les différents mécanismes d'algèbre dynamique afin que l'utilisateur choisisse ceux qu'il veut utiliser. Ces choix sont mémorisés et peuvent être modifiés en sélectionnant à nouveau "Algèbre dynamique : Personnalisé".
Les choix de mécanismes sont des paramètres de l'application. Il est possible de "Voir les paramètres de l'application" avec le menu "Options" et aussi d'afficher un "Tableau des paramètres" qui présente les valeurs de ces paramètres pour tous les modes d'algèbre dynamique. Ce tableau se trouve aussi à :
Il est possible d'associer des paramètres à un document afin que les élèves ne puissent utiliser que certains outils. Voir le manuel d'EpsilonWriter :
Le panneau "Calcul" permet de choisir la forme des explications.
2. Calculs par clic et par bouton
2.1. Calculs exacts par clic sur expression ou utilisation d'un bouton
Le calcul par clic inclut le calcul numérique exact, la factorisation d'entiers, le développement-réduction, la résolution des équations de degré 1, la production des schémas de résolution des équations de degré 2 et 3, les conditions de définition des fonctions rationnelles, le passage de certaines conditions logiques à des ensembles de solutions, le calcul de limites, le passage de fractions rationnelles factorisées à des tableaux de signes, le calcul des dérivées, le passage d'une forme 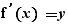 où y est une fraction rationnelle factorisée au tableau de variations.
où y est une fraction rationnelle factorisée au tableau de variations.
Pour faire un calcul exact, on peut sélectionner une expression ou une sous-expression. Si $le mode Calcul par clic est actif et si des calculs sont possibles, ils sont listés dans une bulle d'aide. Lorsqu'il y en a un seul, un clic sur la bulle d'aide applique le calcul proposé. Lorqu'il y en a plusieurs, un Ctrl+Clic sur la sélection fait apparaître un menu pour choisir le calcul à appliquer.
La liste de choix "Dupliquer ..." du panneau Calcul indique si le résultat du calcul doit être affiché à la place, à côté ou en-dessous de l'expression à calculer.
Le choix du domaine (entiers, décimaux ou rationnels) se fait avec une liste de choix du panneau "Calcul".
2.2. Le calcul par clic sur opérateur
Lorsque la souis survole un opérateur, si ce mode est actif et si des calculs sont possibles, ils sont listés dans une bulle d'aide.
Un Ctrl+Clic sur un opérateur demande d'effectuer un calcul sur l'expression de cet opérateur.
Exemple, un Ctrl+Clic sur + dans 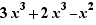 produit
produit 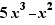
2.3. Les calculs basiques proposés
Des calculs numériques, des développements et des réductions sont proposés, principalement pour les expressions rationnelles.
La résolution d'équations linéaires d'une variable est aussi proposée.
Le bouton  permet d'effectuer des calculs approchés.
permet d'effectuer des calculs approchés.
Les boutons  permettent de convertir des décimaux en fractions et des fractions en décimaux.
permettent de convertir des décimaux en fractions et des fractions en décimaux.
Le bouton  permet de dupliquer l'expression, c'est utile lorsque l'on ne duplique pas l'expression automatiquement pour chaque calcul.
permet de dupliquer l'expression, c'est utile lorsque l'on ne duplique pas l'expression automatiquement pour chaque calcul.
2.4. Calculs proposé pour les polynômes et les équations d'une variable du second degré
Selon les coefficients, les actions suivantes sont proposées pour 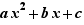 :
:
- Mettre sous forme canonique,
- Factoriser avec 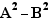 (quand le domaine est
(quand le domaine est  )
)
- Produire les formules du discriminant pour factoriser le polynôme (quand le domaine est  ) .
) .
EpsilonWriter propose aussi de produire les formules du discriminant pour résoudre 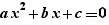 (quand le domaine est
(quand le domaine est 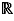 )
)
Voir les démos à : http://epsilonwriter.com
2.5. Calculs proposé pour les polynômes et les équations d'une variable du troisième degré (quand le domaine est 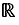 )
)
EpsilonWriter propose de produire les formules de Cardan pour factoriser 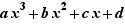 et pour résoudre
et pour résoudre 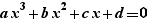
Voir les démos à : http://epsilonwriter.com
2.6. Tableaux de signes (quand le domaine est 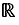 )
)
Pour de nombreuses expressions rationnelles factorisées, comme 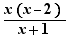 , EpsilonWriter propose de construire un tableau de signe (un tableau rempli ou à remplir).
, EpsilonWriter propose de construire un tableau de signe (un tableau rempli ou à remplir).
2.7. Conditions et ensembles de définition de fonctions (quand le domaine est 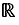 )
)
Quand une fonction est définie avec un signe égal, comme 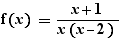 EpsilonWriter propose de produire les conditions de définition, dans l'exemple :
EpsilonWriter propose de produire les conditions de définition, dans l'exemple :
Définie quand: 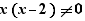
Il est nécessaire ici d'utiliser la véritable notation des fonctions d'EpsilonWriter, c'est-à-dire l'une des lettres f, g et h en forme droite (quand les lettres sont en italique, elles représentent des variables, pas des fonctions).
Quand les conditions de définition sont sous forme factorisée, EpsilonWriter proposes généralement de produire l'ensemble correspondant. Pour la condition ci-dessus :
Ensemble : ]-∞;0[∪]0;2[∪]2;+∞[
2.8. Limites de fractions rationnelles (quand le domaine est 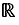 )
)
Pour les limites de fractions rationnelles à l'infini, comme 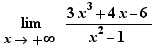 , EpsilonWriter applique le théorème des plus hauts degrés.
, EpsilonWriter applique le théorème des plus hauts degrés.
Pour les limites de fractions rationnelles à des valeurs finies, comme 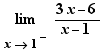 EpsilonWriter remplace la variable x par la notation
EpsilonWriter remplace la variable x par la notation 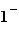 et permet de faire des calculs de limites avec cette notation.
et permet de faire des calculs de limites avec cette notation.
2.9. Calcul de dérivées (quand le domaine est 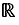 )
)
La notation pour les dérivées peut être 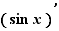 ou
ou 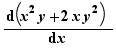
EpsilonWriter calcule une étape de dérivation quand un Ctrl-Click est effectué sur un opérateur de dérivée.
Presque toutes les fonctions usuelles peuvent être dérivées.
2.10. Tableau de variations de fonctions rationnelles (quand le domaine est 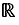 )
)
Quand une dérivée est exprimé sous forme factorisée avec un signe égal, comme 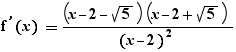 , EpsilonWriter propose généralement de fournir un tableau de variations (un tableau rempli, excepté les limites et les valeurs minimales et maximales, ou un tableau à remplir).
, EpsilonWriter propose généralement de fournir un tableau de variations (un tableau rempli, excepté les limites et les valeurs minimales et maximales, ou un tableau à remplir).
Il est nécessaire ici d'utiliser la véritable notation des fonctions d'EpsilonWriter, c'est-à-dire l'une des lettres f, g et h en forme droite (quand les lettres sont en italique, elles représentent des variables, pas des fonctions).
2.11. Simplification d'ensembles de nombres réels (quand le domaine est 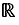 )
)
Les ensembles de nombres réels, exprimés comme combinaisons d'intervalles de d'ensembles finis, comme ![(]-∞;0] \ ]-5;-3[)∩]-8;-1[∪{-6;6}](_Manuel-AD-fr.html/image29.png) peuvent être simplifiés.
peuvent être simplifiés.
3. Le glisser-déposer externe
Fonctionne avec les options "Algèbre dynamique : moyen et fort".
On dit qu'on effectue un glisser-déposer externe lorsque l’expression sélectionnée et l'emplacement pour déposer ne se trouvent pas dans une même expression mathématique, par exemple, s'il l'on a :
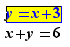
et si l'on effectue un glisser-déposer de l’expression sélectionnée quelque part dans 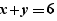 on est en glisser-déposer externe. Il n'y a pas de lien mathématique entre
on est en glisser-déposer externe. Il n'y a pas de lien mathématique entre 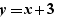 et
et 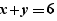 pour EpsilonWriter, il y a juste une équation en dessous d'une autre.
pour EpsilonWriter, il y a juste une équation en dessous d'une autre.
3.1. Le pointage de l'emplacement pour déposer en glisser-déposer externe
Pendant le glisser, lorsque le curseur de la souris :
- survole un élément atomique, celui-ci est montré sous la forme d'une deuxième sélection en bleu,
- survole un opérateur, l'expression de cet opérateur est montrée sous la forme d'une deuxième sélection en bleu,
- n'est pas dans l'un des deux cas précédents, un curseur de dépose est affiché.
Voici quatre exemples de d'indication de l'emplacement pour déposer :
|
|
|
|
Lorsque la dépose est possible, un popup affiche les possibilités sous la forme de l'expression produite et de la description de l'action.
3.2. La réalisation du glisser-déposer externe
Pour accepter une proposition de dépose affichée dans le popup, il faut relâcher le bouton de la souris. S'il y en avait plusieurs propositions, le popup reste affiché et il faut faire un choix en cliquant ou avec la touche entrée ou annuler avec Ctrl+Z.
Code couleur des boutons du popup :
- vert : opération mathématique apportant une équivalence (voir explications dans la section équivalence),
- rouge : opération mathématique n'apportant pas d'équivalence a priori.
Les options :
Dupliquer lors des calculs
Expliquer les calculs
s'appliquent aussi au glisser-déposer externe.
3.3. Les opérations possibles en glisser-déposer externe
Substitution
Lorsque l’expression sélectionnée est une substitution, c'est-à-dire :
- une égalité de la forme 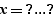 ou
ou 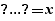 , exemple
, exemple 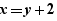
- un système d'égalités de ce type, exemple : 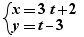 contrexemple :
contrexemple : 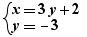 dans ce cas, la variable y exprimée dans la deuxième équation étant présente dans la première équation, le système n'est pas considéré comme une substitution,
dans ce cas, la variable y exprimée dans la deuxième équation étant présente dans la première équation, le système n'est pas considéré comme une substitution,
EpsilonWriter propose d'effectuer la substitution si l'emplacement de la dépose est une expression contenant des variables de la substitution.
Equivalence
Dans ce cas, il y a pas équivalence a priori.
Il y a cependant équivalence dans le cas d'un système d'équations, si la substitution sélectionnée est une équation du système.
Substitution d'une variable par une expression
Lorsque l’expression sélectionnée est une expression, par exemple 4 ou encore 2x+1 , si l'emplacement de la dépose est une variable, EpsilonWriter propose d'effectuer une substitution de la variable par l'expression.
Addition ou soustraction membre à membre de relations
Lorsque l’expression sélectionnée est une égalité ou inégalité et que l'emplacement de la dépose est une égalité ou inégalité,
EpsilonWriter propose une addition et une soustraction membre à membre si cela a du sens, c'est-à-dire si le résultat est impliqué par les deux relations concernées.
Equivalence
Dans ce cas, il y a pas équivalence a priori.
Additionner, soustraire, multiplier, diviser les deux membres d'une relation par une expression
Lorsque l’expression sélectionnée est une expression numérique avec éventuellement des variables (mais pas une relation par exemple) et l'emplacement de la dépose est une égalité ou une inégalité,
EpsilonWriter propose d'additionner, soustraire, multiplier, diviser les deux membres par l'expression.
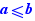
Pour les inégalités, c'est uniquement quand l’expression sélectionnée est un nombre (avec changement du sens de l'inégalité quand le nombre est négatif).
Equivalence
Dans ce cas, il y a équivalence entre la relation initiale et la relation, obtenue sauf dans le cas de multiplication par 0 (la division par zéro n'étant pas proposée). Cette équivalente peut nécessiter l'ajout par l'utilisateur de conditions comme 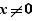 si l'on divise les deux membres d'une égalité par x
si l'on divise les deux membres d'une égalité par x
4. Le glisser-déposer "assimilé" externe
Fonctionne avec les options "Algèbre dynamique : moyen et fort".
Lorsque l'expression sélectionnée et l'emplacement pour déposer sont dans une même formule globales mais dans des égalités ou inégalités ou expressions numériques (avec ou sans variables) on considère que l'on est dans une situation semblable à celle du glisser-déposer externe et le comportement général du glisser-déposer est le même.
C'est le cas de systèmes d'équations ou d'inéquations :
Exemple : 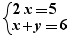 si on dépose
si on dépose 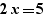 sur y ou sur
sur y ou sur 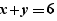
Dans le cas d'un système d'équations ou d'inéquations, il y a toutefois une différence au niveau de l'équivalence :
- dans le cas d'une substitution, il y a équivalence entre le système d'origine et le système obtenu,
- dans le cas "Addition ou soustraction membre à membre de relations", il y a équivalence entre le système d'origine et le système obtenu si la relation ajoutée ou soustraite est une égalité.
5. Le glisser-déposer interne
Lorsque l'expression sélectionnée et l'emplacement pour déposer sont dans une même expression numérique (avec ou sans variables) ou dans une même égalité ou inégalité, on est dans le cas du glisser-déposer interne.
Le glisser-déposer interne fonctionne selon l'option "Algèbre dynamique" :
- Avec l'option "Algèbre dynamique : pédagogique", seuls les mouvements basiques sont proposés. Un mouvement basique d'une expression a est un mouvement qui conserve a ou le remplace par -a ou par 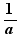 , et qui conserve le reste de l'expression avec une exception possible: s'il y a une inégalité, son sens peut être inversé. Avec cette option, les gestes qui ne produisent pas de mouvement basique sont indiqués.
, et qui conserve le reste de l'expression avec une exception possible: s'il y a une inégalité, son sens peut être inversé. Avec cette option, les gestes qui ne produisent pas de mouvement basique sont indiqués.
- Avec l'option "Algèbre dynamique : faible", les mouvements simples et utiles (basiques ou non) sont proposés.
- Avec l'option "Algèbre dynamique : moyen", les mouvements proposés sont plus nombreux.
- Avec l'option "Algèbre dynamique : fort", tous les mouvements possibles avec EpsilonWriter sont proposés.
Voir la liste détaillée des mouvements possibles pour chaque option sur http://epsilonwriter.com
L'option "Décrire le geste d'algèbre dynamique" permet de décrire certains gestes. Cette description est ajoutée à l'explication mathématique.
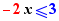
Exemple : le déplacement d'un facteur négatif d'un membre à l'autre d'une inéquation fournit la description et l'explication ci-dessous :
|
Geste : Passage multiplicatif d'une expression négative dans l'autre membre, le facteur devient diviseur, changement de sens de l'inégalité Explication : Division des deux membres par -2 |
Le pointage de l'emplacement pour déposer en glisser-déposer interne, sa réalisation et son affichage
Le pointage de l'emplacement pour déposer a deux formes possibles :
- d'un curseur, par exemple  pour dépose devant 4 ce qui produit le résultat
pour dépose devant 4 ce qui produit le résultat 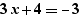
- une expression sélectionnée en bleu pour une combinaison de l'expression déplacée avec celle-ci, par exemple  qui produit le résultat
qui produit le résultat 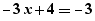
Lorsque la dépose est possible, un popup affiche les possibilités. Il affiche aussi des déposes d'édition ordinaire avec les opérateurs principaux.
En glisser-déposer interne, il y a toujours équivalence, mais cette équivalence peut nécessiter l'ajout par l'utilisateur de conditions comme 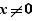 si l'on divise les deux membres d'une égalité par x
si l'on divise les deux membres d'une égalité par x
Avec l'option Algèbre dynamique pédagogique, certaines déposes refusées sont décrites. Par exemple, avec 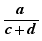 , si l'on essaie de déplacer c devant la fraction on obtient : Pas de sortie additive du dénominateur
, si l'on essaie de déplacer c devant la fraction on obtient : Pas de sortie additive du dénominateur
Les opérations de glisser-déposer interne
Les opérations élémentaires actuellement implantées entrent dans 4 catégories :
- déplacement de l'expression sélectionnée dans une expression,
- sortie de l'expression sélectionnée d'une expression,
- entrée de l'expression sélectionnée dans une expression,
- combinaison de l'expression sélectionnée avec une autre expression.
Ces opérations se font avec un statut de l'expression sélectionnée qui peut être :
- additionneur : on parlera aussi de terme additif ou d'opération additive,
- multiplicateur : on parlera aussi de facteur ou d'opération multiplicative,
- diviseur,
- exposant.
Dans de très nombreux cas, ces opérations élémentaires peuvent se cumuler.
Pendant le glisser, lorsque l'on est dans un cas de combinaison, le deuxième élément de la combinaison est montré sous la forme d'une deuxième sélection en bleu. Dans les autres cas, un curseur de dépose est affiché.
5.1. Exemples de déplacements
Un argument d'une somme ou d'un produit peut être déplacé dans cette somme ou ce produit.
|
Explication : Commutativité |
Un membre d'une relation, ou un terme additif d'un membre, peut être déplacé de façon additive dans l'autre membre. Il est remplacé par son opposé.
|
Geste : Passage additif dans l'autre membre en changeant de signe Explication : Addition aux deux membres de -2x |
Un membre d'une relation, ou un facteur d'un membre, peut être déplacé de façon multiplicative dans l'autre membre. Il doit être non nul. Dans le cas d'une inégalité, il ne doit pas contenir de variable. Il devient diviseur. Le sens de la relation est inversé si nécessaire.
|
Geste : Passage multiplicatif d'une expression négative dans l'autre membre, le facteur devient diviseur, changement de sens de l'inégalité Explication : Division des deux membres par -4 |
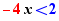
Si l'on déplace 4x dans 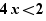 , il n'y a pas de proposition comme diviseur car 4x n'est pas constant.
, il n'y a pas de proposition comme diviseur car 4x n'est pas constant.
Un exposant 2 d'un membre d'une égalité peut être déplacé dans l'autre membre si ce dernier est une expression sans variable. Il y a alors production d'une racine carrée et d'un "ou" entre deux égalités.
|
Explication : Décomposition d'une équation |
5.2. Exemples de sorties d'une expression
Un terme d'une somme ou un facteur d'un terme d'une somme, peut sortir de la somme comme facteur. Il doit être non nul.
|
Explication : Mise en facteur de x |
Un numérateur ou un facteur d'un numérateur peut être déplacé en dehors de la fraction.
|
Explication : Le facteur 2 du numérateur devient facteur de la fraction |
PGCD en facteur
Lorsque l'on demande de mettre en facteur un nombre entier positif n dans un somme, si les termes de la sommes ont des coefficients admettant un PGCD différent de 1 et de n , EpsilonWriter propose aussi de mettre le PGCD en facteur.
|
Explication : PGCD en facteur : 3 |
5.3. Exemples d'entrée dans une expression
Un facteur peut entrer dans une somme, un développement est alors effectué.
|
Explication : Développement |
Un facteur d'une fraction peut entrer dans le numérateur.
|
Explication : Multiplication par 2 de la fraction en multipliant le numérateur |
Un diviseur peut entrer dans une somme, un développement est alors effectué (si le diviseur est a on distribue l'inverse de a ).
Exemple, en combinaison avec un déplacement dans une égalité :
|
Geste : Passage multiplicatif dans l'autre membre, le facteur devient diviseur Explication : Division des deux membres par 4 |
|
Explication : Développement |
Un exposant 2 ou 3 portant sur une somme de deux termes peut entrer dans la somme, un développement est alors effectué
|
Développement |
Un exposant portant sur un produit, un opposé ou une puissance peut entrer dans son argument
|
Puissance d'un opposé |
5.4. Le cas du signe -
Un signe - sélectionné peut faire l'objet d'un glisser-déposer, tout se passe comme si -1 avait été sélectionné avec un statut de facteur.
|
Explication : Développement |
5.5. Combinaisons : combinaisons additives
Notion de termes semblables
Deux termes d'une somme sont semblables lorsque chacun est de l'une des formes 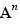 ,
, 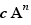 , avec le même A et le même n , A étant une expression quelconque, c un nombre et n un nombre entier qui peut être omis s'il vaut 1.
, avec le même A et le même n , A étant une expression quelconque, c un nombre et n un nombre entier qui peut être omis s'il vaut 1.
Exemples :
x , -x , 3x , 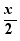 ,
, 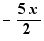 ,
, 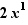 sont des termes semblables
sont des termes semblables
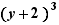 ,
, 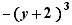 ,
, 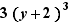 ,
, 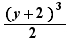 ,
, 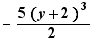 sont des termes semblables
sont des termes semblables
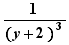 ,
, 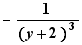 ,
, 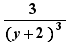 ,
, 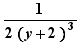 ,
, 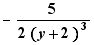 sont des termes semblables
sont des termes semblables
Lorsque l'option "Combinaison d'exposants positifs et négatifs" est activée, 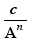 et
et 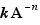 avec le même A et le même n sont aussi considérés comme des termes semblables
avec le même A et le même n sont aussi considérés comme des termes semblables
Un terme d'une somme peut être déplacé dans cette somme sur un terme semblable pour que les deux soient remplacés par leur somme calculée.
Le calcul du coefficient tient compte de l'option "Calculer (exact...)".
|
Addition de termes semblables |
Un terme d'une somme de la forme nA peut être déplacé dans cette somme sur un terme de la forme 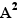 pour produire une forme canonique
pour produire une forme canonique
|
Début d'un carré |
5.6. Combinaisons : combinaisons multiplicatives
Notion de facteurs semblables
Deux facteurs d'un produit sont semblables lorsque chacun est de l'une des formes A , 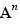 , avec le même A , A étant une expression quelconque, n un nombre entier.
, avec le même A , A étant une expression quelconque, n un nombre entier.
Exemples :
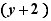 ,
, 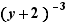 ,
, 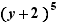 sont des facteurs semblables
sont des facteurs semblables
Lorsque l'option "Combinaison d'exposants positifs et négatifs" est activée, A , 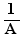 ,
, 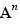 ,
, 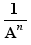 avec le même A sont des facteurs semblables
avec le même A sont des facteurs semblables
Un facteur d'un produit peut être déplacé dans ce produit sur un facteur semblable pour que les deux soient remplacés par leur produit calculé.
|
Multiplication de facteurs semblables |
5.7. Combinaisons : simplifications des fractions
Un nombre entier facteur au numérateur/dénominateur d'une fraction peut être déplacé sur un nombre entier facteur au dénominateur/numérateur de la fraction pour que les deux soient simplifiés par leur PGCD.
|
Simplification par 6 |
Une expression de la forme X ou 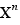 facteur au numérateur/dénominateur d'une fraction peut être déplacée sur une expression de la forme X ou
facteur au numérateur/dénominateur d'une fraction peut être déplacée sur une expression de la forme X ou 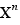 facteur au dénominateur/numérateur de la fraction pour que les deux soient simplifiées par
facteur au dénominateur/numérateur de la fraction pour que les deux soient simplifiées par 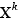 avec k maximum.
avec k maximum.
|
Simplification par |
Qu'est-ce que "être facteur au numérateur" dans les cas ci-dessus ?
C'est être X dans l'une des formes 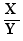
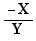
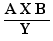
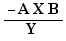 , idem pour le facteur au dénominateur.
, idem pour le facteur au dénominateur.
5.8. Combinaisons : simplifications multiplicatives des relations
Des simplifications analogues aux simplifications des fractions peuvent être effectuées sur les relations.
Pour les inégalités : il faut que l'expression par laquelle on simplifie soit constante et lorsque son signe est négatif, le sens de l'inégalité est inversé.
Attention : lorsque la simplification est faite par une expression non constante dans une équation, il y a généralement perte de solutions, par exemple, si l'on simplifie l'équation  par x on perd la solution
par x on perd la solution 
C'est à l'utilisateur de gérer les conditions qui accompagnent les opérations. Dans le cas ci-dessus, l'utilisateur peut ajouter "quand  " et gérer par ailleurs le cas
" et gérer par ailleurs le cas  . Il peut aussi ne pas faire l'opération et faire un traitement ne séparant pas des cas.
. Il peut aussi ne pas faire l'opération et faire un traitement ne séparant pas des cas.
Exemple, on sélectionne un signe - par Ctrl+Clic et on le déplace sur l'autre signe -
|
Simplification des signes moins |
|
Division des deux membres par x |
5.9. Combinaisons : simplifications additives des relations
Des simplifications additives analogues aux combinaisons additives dans les sommes peuvent être effectuées sur les relations.
|
Addition aux deux membres de 5x |
6. L'équivalence
L'équivalence indiquée par EpsilonWriter dans le popup et les explications :
Quand il y a équivalence, les boutons sont verts dans le popup et la flèche de l'explication est sinueuse et verte : 
L'équivalence mentionnée dans les glisser-déposer interne et externe est une équivalence apportée par le contexte et l'interprétation du geste :
Dans certains contextes, on sait qu'il y a équivalence modulo des conditions à ajouter le cas échéant
De façon plus précise :
Quand il y a indication d'équivalence, c'est que le contexte (interne ou externe, nature de la transformation effectuée, nature des expressions sur lesquelles elle opère) permettent de l'affirmer, modulo des conditions à ajouter le cas échéant.
Attention, il peut parfois y avoir équivalence quand le contexte ne l'indique pas, par exemple, dans le système d'inéquations 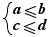 l'ajout membre à membre des inéquations qui produit
l'ajout membre à membre des inéquations qui produit 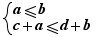 n'est pas une opération apportant l'équivalence, seulement une implication, mais dans le cas particulier
n'est pas une opération apportant l'équivalence, seulement une implication, mais dans le cas particulier 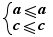 il y a quand même équivalence et EpsilonWriter ne l'indique pas. Donc l'équivalence indiquée n'est pas une équivalence entre expression initiale et expression transformée (comme c'est le cas dans Aplusix) mais une équivalence apportée par le contexte et la nature du geste.
il y a quand même équivalence et EpsilonWriter ne l'indique pas. Donc l'équivalence indiquée n'est pas une équivalence entre expression initiale et expression transformée (comme c'est le cas dans Aplusix) mais une équivalence apportée par le contexte et la nature du geste.
7. Les explications
7.1. Signification des flèches
L'explication avec la flèche droite → ci-dessous :
|
Addition membre à membre de |
se lit :
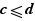 a été remplacé par
a été remplacé par 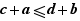 . La flèche → indique le remplacement, rien de plus.
. La flèche → indique le remplacement, rien de plus.
L'explication avec la flèche sinueuse  ci-dessous :
ci-dessous :
|
Explication : Développement |
se lit 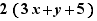 a été remplacé par 6x+2y+10 en effectuant l'opération " développement " et il y a équivalence avec éventuellement des conditions à ajouter.
a été remplacé par 6x+2y+10 en effectuant l'opération " développement " et il y a équivalence avec éventuellement des conditions à ajouter.
Dans ce cas, l'équivalence peut se trouver entre les deux expressions mentionnées ou au niveau d'un système d'équations et inéquations qui contient les deux arguments de l'opération (application d'une substitution, ajout ou soustraction membre à membre).
7. 2. Le code couleur
Pour les déplacements, entrées, sorties, la couleur rouge indique l'élément déplacé.
Exemple :
|
Division des deux membres par 2 |
Dans certains cas, l'élément ne se retrouve pas dans le résultat, c'est une opération plus complexe qui est effectuée, son résultat est indiqué en marron, exemple :
|
Développement |
8. Défaire
Lorsque l'on ne fait pas de duplication et que l'on ne demande pas d'explication, le résultat de l'opération remplace simplement l'expression. Dans ce cas, "défaire" (Ctrl+Z) replace dans la situation précédent l'opération.
Lorsque l'on effectue une duplication ou que l'on demande une explication, il y a production de lignes complémentaires. Dans ce cas, un premier "défaire" place dans la situation "opération sans duplication et sans explication" et un deuxième "défaire" replace dans la situation précédent l'opération.
9. Supprimer, modifier des explications
Les explications sont fournies dans un paragraphe ou dans un tableau. Elles sont modifiables.
10. Génération de formules
10.1. Principe
L'opérateur spécial de formules "pour" permet d'écrire une formule avec des paramètres pour que engendrer ensuite des formules en instanciant des paramètres. Par exemple, si l'on écrit la formule :
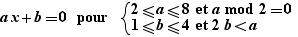
et si l'on effectue un Ctrl+Clic sur pour, on obtient :
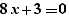
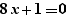
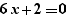
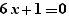
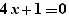
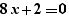
sur la ligne en-dessous.
Le panneau de bouton "Génération" donne accès à des outils pour la génération de formules.
10.2. Les deux façons d'engendrer des formules
La première façon consiste à effectuer un Ctrl+Clic sur le pour. Le résultat s'ajoute sur la ligne en-dessous.
La deuxième façon consiste à utiliser le bouton "Générer" du panneau "Génération". La génération concerne alors un paragraphe ou un tableau qu'il faut sélectionner auparavant (on peut se contenter de sélectionner une partie du paragraphe ou du tableau).
Exemple dans le cas d'un paragraphe avec la ligne ci-dessous :
L'équation 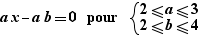 a pour solution b
a pour solution b
En sélectionnant une partie de la ligne et en cliquant sur "Générer", on obtient :
L'équation 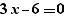 a pour solution 2
a pour solution 2
L'équation 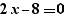 a pour solution 4
a pour solution 4
L'équation 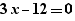 a pour solution 4
a pour solution 4
L'équation 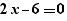 a pour solution 3
a pour solution 3
L'équation 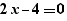 a pour solution 2
a pour solution 2
L'équation 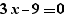 a pour solution 3
a pour solution 3
A noter que le résultat remplace la ligne d'origine.
Exemple dans le cas d'un tableau (les petits cadres bleus sont expliqués plus loin) :
La fraction |
se simplifie par |
le résultat est |
|
a |
|
En sélectionnant une partie du tableau et en cliquant sur "Générer", on obtient un tableau dont le début est :
La fraction |
se simplifie par |
le résultat est |
|
3 |
|
|
2 |
|
|
2 |
|
Remarques :
- le résultat remplace le tableau d'origine,
- si le tableau comporte plusieurs lignes : chaque ligne qui ne contient pas de pour est copiée dans le résultat ; chaque ligne qui contient un pour est développée dans le résultat.
10.3. Syntaxe et fonctionnement des "pour"
Un pour comporte des paramètres. Ce sont les lettres qui se trouvent à droite, dans une double inégalité avec des bornes entières, par exemple : 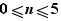 . Cela signifie que n est un paramètre et que ses valeurs initiales sont les entiers exprimés par cette formule. Les lettres possibles pour les paramètres sont les lettres latines et grecques, minuscules ou majuscules, à l'exception des deux constantes e et π .
. Cela signifie que n est un paramètre et que ses valeurs initiales sont les entiers exprimés par cette formule. Les lettres possibles pour les paramètres sont les lettres latines et grecques, minuscules ou majuscules, à l'exception des deux constantes e et π .
La partie droite de "pour" peut combiner les trois formes de "et" : 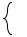
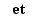 ∧ de façon quelconque.
∧ de façon quelconque.
Les conditions qui ne définissent pas les valeurs initiales des paramètres peuvent comporter des 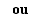 et des non
et des non
Les formules engendrées sont ordonnées au hasard.
L'opérateur spécial nombre permet de limiter le nombre de formules à engendrer. Par exemple :
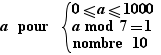
fournit 10 nombres entre 0 et 1000 dont le reste de la division par 7 est égal à 1.
Il est possible d'utiliser les opérateurs mod (modulo, reste de la division), pgcd et ppcm qui sont très utiles dans certains cas.
Il est possible aussi d'utiliser l'opérateur logique premier , 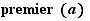 est vrai quand a est un nombre premier.
est vrai quand a est un nombre premier.
L'opérateur soit, utilisable dans la partie droite du pour, permet de construire des formules intermédiaires.
Par exemple dans le pour du tableau ci-dessous, on exprime, dans des paramètres construits par des soit, des valeurs qu'on utilise dans certaines cellule :
fraction |
simplification par |
numérateur simplifié |
dénominateur simplifié |
fraction simplifiée |
|
p |
n |
d |
|
"Générer" appliquer à ce tableau fournit un tableau qui commence par :
fraction |
simplification par |
numérateur simplifié |
dénominateur simplifié |
fraction simplifiée |
|
2 |
4 |
3 |
|
|
2 |
1 |
4 |
|
10.4. Ordre des conditions
Les doubles inégalités qui définissent les valeurs initiales des paramètres doivent être placées en premier.
Les conditions qui portent sur des paramètres définis par des "soit" doivent être placées après les "soit" définissant ces paramètres.
10.5. Les opérateurs  et
et 
Lors de la génération d'un pour, les calculs simples sont effectués sur les expressions. Ainsi, la génération de 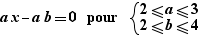 fournit
fournit
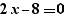
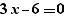
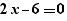
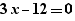
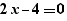
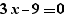
et non :
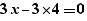
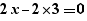
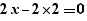
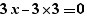
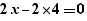
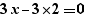
Les opérateurs  et
et  sont des opérateurs de calcul. Lorsqu'on en place sur des sous-expressions, cela signifie "effectuer les calculs simples" sur les parties encadrées et ne pas les effectuer ailleurs.
sont des opérateurs de calcul. Lorsqu'on en place sur des sous-expressions, cela signifie "effectuer les calculs simples" sur les parties encadrées et ne pas les effectuer ailleurs.
Leur différence concerne les nombres décimaux : avec l'opérateur bleu, ils sont mis sous la forme de fractions ; avec l'opérateur rose, ils sont exprimés avec la notation décimale.
Ceci est illustré par le tableau ci-dessous :
fraction non simplifiée |
fraction simplifiée sous forme de fraction |
notation décimale si possible |
|
|
|
dont la génération fournit un tableau qui commence par :
fraction non simplifiée |
fraction simplifiée sous forme de fraction |
notation décimale si possible |
|
|
0,5 |
|
|
0,75 |
|
|
|
Remarque : dans l'exemple ci-dessus,  demande de ne pas faire les calculs simples sur a et b , mais il n'y en a pas à faire car ce sont des entiers, mais cela demande aussi de ne pas faire les calculs simples ailleurs, de ne pas simplifier la fraction.
demande de ne pas faire les calculs simples sur a et b , mais il n'y en a pas à faire car ce sont des entiers, mais cela demande aussi de ne pas faire les calculs simples ailleurs, de ne pas simplifier la fraction.